Postulats et théorèmes

5.1 Postulats d'Euclide
En plus de l'intérêt pratique de la géométrie euclidienne, les anciens Grecs trouvaient aussi une valeur esthétique à l'étude de la géométrie. Comme des enfants assemblent des cubes pour faire des tours, les mathématiciens assemblent des définitions et des assertions en de nombreux théorèmes. Les cubes sont assemblés avec les mains, les postulats avec la raison.

Toute la géométrie euclidienne (des milliers de théorèmes) est assemblée avec 5 sortes de "cubes". Ce sont les "Cinq postulats d'Euclide":

P-1 Chaque couple de points définit exactement une droite.
P-2 Tout segment d'extrémités données peut être prolongé dans chaque direction.
P-3 Il est possible de construire un cercle avec n'importe quel point comme centre et n'importe quelle longueur comme rayon. (Ceci implique qu'il n'y a pas de bornes inférieure ou supérieure à la distance. Autrement dit, n'importe quelle distance, aussi grande soit-elle peut toujours être augmentée, et n'importe quelle distance, aussi petite soit-elle peut être partagée.)
P-4 Si deux droites se coupent suivant des angles adjacents égaux, chacun de ces angles est aussi égal à tout autre angle ayant la même origine.
P-5 ( Postulat des parallèles): Etant donnés une droite L et un point en dehors de L, il existe une droite et une seule qui passe par le point, soit dans le même plan que L et lui soit parallèle.

Le but d'Euclide était que ces postulats soient peu nombreux et si évidents qu'ils ne puissent être remis en cause. Pendant 2000 ans, beaucoup de gens pensaient que le cinquième postulat (Postulat des parallèles) n'était pas nécessaire. Ils croyaient qu'il pouvait être démontré comme un théorème à partir des quatre premiers et beaucoup essayèrent. Il fallut attendre le 19° siècle avec Lobachevski (1793-1856), Bolyai (1777-1855) et Gauss (1802-1860) pour mettre fin à cette impossible recherche. Lobachevski développa des théorèmes en utilisant les 4 premiers postulats d'Euclide et la négation du postulat des parallèles. Son objectif était de développer deux théorèmes qui seraient contradictoires. Ceci aurait prouvé que la négation du postulat des parallèles était contradictoire avec les quatre premiers postulats - ce qui aurait prouvé le postulat des parallèles (et en aurait fait un théorème). A sa surprise, il n'obtint jamais de contradiction. A la place, il développa une géométrie complète et cohérente - la première géométrie non-euclidienne. Ceci prouve que le postulat des parallèles ne peut être déduit des quatre autres. C'était d'un grand intérêt mathématique et philosophique. Depuis l'Antiquité, la croyance que les théorèmes géométriques étaient pure vérité parfaite faisait qu'ils n'avaient pas besoin d'être confrontés aux observations du monde réel. Maintenant, ceci n'est plus le fait que de quelques géométries. La seule raison de préférer une géométrie à une autre est par référence au monde réel. En dépit de son intérêt philosophique et esthétique, on croyait la géométrie non-euclidienne sans intérêt pratique. Mais au début du siècle, Einstein (1878-1955) développa la théorie de la relativité générale qui fit un usage important d'une géométrie non-euclidienne appelée géométrie hyperbolique. Cette abstraction mathématico-philosophique était maintenant dans la réalité scientifique.

La géométrie hyperbolique est une géométrie non-euclidienne basée sur les 4 premiers postulats d'Euclide avec les différences suivantes sur le postulat des parallèles.

5.2 Postulat des parallèles en géométrie hyperbolique:
Etant donné une droite L et un point non situé sur L, il y a au moins 2 droites L1 et L2 qui passent par le point, sont dans le même plan que L et lui sont parallèles.

5.3 Postulat SAS:
Le postulat SAS est un sixième postulat requis à la fois en géométrie euclidienne et en géométrie hyperbolique.

Le postulat SAS affirme que si deux côtés et l'angle formé par les deux côtés d'un triangle sont égaux à ceux d'un autre triangle, les deux triangles sont égaux.

Dans les Elements, Euclide présente ce qu'il croit être une démonstration de SAS:[Health-56]

Données:
DABC et DDEF, avec AB @ DE, AC @ DF, et Ð A @ Ð D.

Démonstration:
Déplacer DABC pour que le point A coïncide avec le point D, et la droite (AB) coïncide avec (DE).
Le point B coïncidera avec E, car AB @ DE.
Aussi, la droite (AC) coïncidera avec (DF), car ÐA @ ÐD.
Le point C coïncidera avec F, car AC @ DF.
La droite (BC) coïncidera avec (EF), car les deux droites ne peuvent inclure un espace.
Finalement, BC est égal à EF, car les segments et leurs extrémités coïncident.
D'où, ÐB @ ÐE, ÐC @ ÐF, and DABC @ DDEF.

La faille dans ce raisonnement est de l'utilisation de "déplacer". Si "déplacer" (en géométrie hyperbolique et euclidienne) est défini comme une fonction qui envoie un ensemble de points, P1, P2, P3, ... en P'1, P'2, P'3..., de sorte que pour tout couple de points Pn et Pm de l'ensemble de départ, la distance de Pn à Pm est égale à la distance de P'n à P'm. Ensuite, pour avoir SAS, il faut que pour deux droites quelconques L et L', il soit toujours possible de "déplacer" la droite L pour qu'elle coïncide avec L'. Cette condition est communément appelée postulat SAS, c'est le sixième postulat en géométrie euclidienne et en géométrie hyperbolique . [Moise-74]

5.4 Théorèmes de géométrie hyperbolique:
En plus de ces postulats, géométrie euclidienne et géométrie hyperbolique requièrent un certain nombre d'affirmations comme "Des objets qui sont égaux au même objet sont aussi égaux entre eux" et "de trois points quelconques sur une droite, un seul est entre les deux autres." Toutes ces notions sont les mêmes dans les deux géométries. En fait, la seule différence entre l'axiomatique complète de la géométrie euclidienne et celle de la géométrie hyperbolique est le postulat des parallèles.

C'est extraordinaire. Cela signifie que tout théorème de géométrie euclidienne qui n'utilise pas le postulat des parallèles est aussi un théorème en géométrie hyperbolique!

De même, il semble que les théorèmes de géométrie euclidienne qui utilisent le postulat des parallèles soient faux en géométrie hyperbolique. Un exemple: en géométrie euclidienne un théorème dit que la somme des angles d'un triangle est toujours égale à 180º. La figure 5.4a vous rappelle la démonstration de ce théorème - et montre que c'est faux en géométrie hyperbolique.

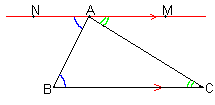
Figure 5.4a: Preuve pour mÐA + mÐ B + mÐ C = 180º

En géométrie euclidienne, pour tout DABC, il existe une unique parallèle à BC qui passe par le point A. Ensuite, Ð NAB @ Ð ABC et Ð MAC @ Ð ACB comme angles alterne-internes sur une sécante coupée par un couple de parallèles. En géométrie hyperbolique, il y a une infinité de droites qui sont parallèles à BC et passent par le point A, aussi il n'existe aucune droite telle que l'on ait à la fois:
Ð NAB @Ð ABC et Ð MAC @ Ð ACB.

Accueil NonEuclid
Suivant - Aire