Aire

6.1 A=½bh

En géométrie euclidienne, l'aire d'un triangle est obtenue en multipliant la longueur d'un côté par celle de la hauteur correspondante et en divisant le produit par 2 (A=½bh). L'exemple ci-dessous illustre ce calcul en géométrie hyperbolique.

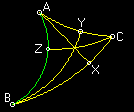
Figure 6.1: Hauteurs du Triangle

Le triangle ABC est un triangle quelconque. Les segments AX, BY, and CZ sont les 3 hauteurs du triangle ABC. Remarquez que, comme en géométrie euclidienne, les 3 hauteurs sont concourantes.
En mesurant sur ce triangle particulier, nous avons:

base AB = 3.3, hauteur CZ = 1.1
base BC = 3.0, hauteur AX = 1.9
base AC = 2.1, hauteur BY = 2.5
Angle AXB = Angle AXC = 90°
Angle BYA = Angle BYC = 90°
Angle CZA = Angle CZB = 90°

Si nous calculons l'aire avec A=½bh, nous trouvons que ½(AB)x(CZ) n'est pas égal à ½(AB)x(CZ). En géométrie hyperbolique, la formule A=½bh donne 3 réponses différentes suivant le côté choisi.
Comme la formule A=½bh donne 3 réponses différentes en géométrie hyperbolique, elle ne peut être utilisée pour calculer l'aire.

6.2 A=s²
En géométrie euclidienne, nous définissons un carré de côté 1 pour avoir une aire d'une unité. En géométrie hyperbolique, les rectangles (quadrilatères avec 4 angles droits) n'existent pas et donc les carrés (cas particulier de rectangle avec des côtés égaux) non plus. En géométrie hyperbolique, si un quadrilatère a 3 angles droits, alors le quatrième doit être aigu. (voir figure 6.2a).

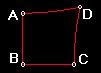
Figure 6.2a: Quadrilatère avec 3 Angles droits & 1 Angle aigu

Un quadrilatère régulier est un quadrilatère qui a 4 côtés de même longueur, et 4 angles égaux. Un carré est un cas particulier de quadrilatère régulier dans lequel les 4 angles sont des angles droits. En géométrie euclidienne, tous les quadrilatères réguliers sont des carrés. En géométrie hyperbolique, les quadrilatères réguliers existent, mais ils ont 4 angles aigus. Les quadrilatères réguliers en géométrie hyperbolique ne peuvent servir d'unité d'aire comme les carrés en géométrie euclidienne. Une raison en est que pour la géométrie hyperbolique, les quadrilatères réguliers accolés laissent des vides. La figure 6.2b montre comment 9 quadrilatères réguliers de 1x1 forment en géométrie euclidienne un carré 3x3 quadrilatère régulier. La figure 6.2c montre 5 quadrilatères réguliers de 1x1 en géométrie hyperbolique - remarquez le vide.

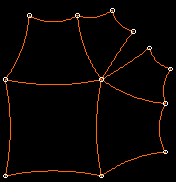
Figure 6.2: Quadrilatères réguliers en (b) géométrie euclidienne, et (c) géométrie hyperbolique

Construction de pavages avec des quadrilatères par un élève de 1°S

6.3 Déficit du triangle
Comme nous l'avons vu, en géométrie hyperbolique, la somme des trois angles du triangle est toujours inférieure à 180°. Le déficit du triangle est défini comme 180° moins la somme des 3 angles du triangle. Quand nous construisons quelques triangles hyperboliques, et mesurons le déficit de chacun, nous trouvons que pour de petits triangles le déficit est faible (la somme des angles est proche de 180°). En fait, quand le périmètre du triangle approche zéro, la somme des angles approche 180°. Ceci est cohérent avec l'idée qu'une très petite partie de l'espace hyperbolique ressemble et se comporte comme l'espace euclidien. A contrario, nous trouvons que de grands triangles ont un fort déficit. Quand la longueur des 3 côtés du triangle approche de plus en plus de l'infini, chacun des angles approche de plus en plus de zéro degrés - et, donc le déficit approche de plus en plus de 180°.

Avant de conclure, il serait intéressant de construire quelques triangles dans NonEuclid. En utilisant "Measure Triangle" du menu "Measurement": cette commande affichera la mesure des angles et la longueur des côtés. Il est important de "sentir" que de grands triangles ont un déficit important.

Vous pouvez travailler sur une figure interactive pour vérifier ceci

Plus le triangle est grand, plus le déficit est important - mais mieux: comme pour les aires, les déficits s'ajoutent. Le tout est la somme des parties. Par exemple, dans la figure 6.3, le déficit de DBAM est 77.4°, celui de DCAM est 43.7°, et le déficit de DABC est 121.1° (77.4 + 43.7 = 121.1). Ceci est vrai pour tous les triangles en géométrie hyperbolique - indépendamment de la manière dont on les découpe en triangles plus petits. Utilisez NonEuclid sur quelques exemples.

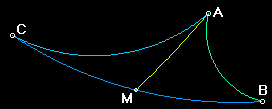
Figure 6.3: Additivité du déficit

6.4 Déficit d'un polygone
Tout polygone peut être décomposé en un nombre fini de triangles qui ne se recouvrent pas. La figure 6.4 montre 2 manières différentes de découper le même polygone.

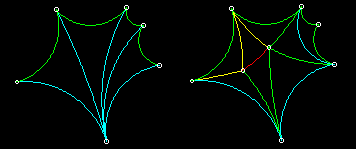
Figure 6.4: Deux décompositions d'un polygone

Le déficit d'un polygone est défini comme la somme des déficits des triangles qui le composent. Un polygone peut être découpé en régions triangulaires d'une infinité de manières (pour faire court, seules 2 manières sont montrées ci-dessus). De toute façon, la somme dépend uniquement du polygone de départ et est indépendante de la manière de découper. Essayez et mesurez quelques exemples.

6.5 Invariance du déficit par translation
Nous avons déjà vu que les objets semblaient rétrécir et s'étirer quand du centre nous allions vers la frontière du cercle. La mesure de l'aire doit rester invariante quand un objet se déplace d'un endroit à un autre. Rappelez vous qu'en dépit du fait que les objets semblent rétrécir, les mesures des côtés et des angles restent constantes quand l'objet bouge. Donc, le déficit reste constant quand un objet se déplace (puisque le déficit ne dépend que de la mesure des angles).

6.6 Propriétés nécessaires pour une fonction d'aire
En résumé, une fonction d'aire doit avoir les propriétés suivantes [Moise-74]:

A-1. On doit pouvoir mesurer l'aire d'une région polygonale quelconque.
A-2. Pour chaque région polygonale, l'aire doit être un nombre réel positif.
A-3. Si deux régions triangulaires sont égales, elles doivent avoir même aire.
A-4. Si deux régions polygonales n'ont en commun que des côtés et des sommets (ou rien du tout), alors l'aire de leur réunion est la somme de leurs aires.

Il peut être démontré que toute fonction qui satisfait A-1 à A-4 est de la forme d'une constante (k) multipliée par le déficit (d) ou A=kd . [Moise-74]

Le choix de la constante, k, est important. C'est ce qui liera les unités de longueur aux unités d'aire.

6.7 Maximum pour l'aire
Une conséquence intéressante de A=kd, est que l'aire maximum d'un triangle est bornée. En effet le déficit d'un triangle ne peut dépasser 180°, l'aire ne peut dépasser k(180). Est-il aussi vrai que l'aire d'un polygone est bornée? On peut argumenter que l'aire d'un polygone sera bornée comme ceci: supposez que vous construisez un polygone avec un déficit de 200°. Ensuite construisez un triangle qui inclut complètement ce polygone. Le déficit de ce triangle est égal à la somme des déficits de chacune de ses parties, aussi le déficit de ce triangle doit dépasser 200° - ce qui est impossible. Aussi, il doit être impossible pour un polygone d'avoir un déficit de 200°. Toutefois, ceci n'est pas une démonstration car il y a une affirmation - voir les exercices sur les polygones pour plus de détails.

Accueil NonEuclid
Suivant - Coordonnées cartésiennes